DZERO refutes CDF’s multimuon signal… Or does it ? March 17, 2009
Posted by dorigo in news, physics, science.Tags: anomalous muons, CDF, DZERO, new physics, standard model, Tevatron
comments closed
Hot off the press: Mark Williams, a DZERO member speaking at Moriond QCD 2009 -a yearly international conference in particle physics, where HEP experimentalists regularly present their hottest results- has shown today the preliminary results of their analysis of dimuon events, based on 900 inverse picobarns of proton-antiproton collision data. And the conclusion is…
DZERO searched for an excess of muons with large impact parameter by applying a data selection very similar, and when possible totally equivalent, to the one used by CDF in its recent study. Of course, the two detectors have entirely different hardware, software algorithms, and triggers, so there are certain limits to how closely one analysis can be replicated by the other experiment. However, the main machinery is quite similar: they count how many events have two muons produced within the first layer of silicon detector, and extrapolate to determine how many they expect to see which fail to yield a hit in that first layer, comparing to the actual number. They find no excess of large impact parameter muons.
Impact parameter, for those of you who have not followed this closely in the last few months, is the smallest distance between a track and the proton-antiproton collision vertex, in the plane transverse to the beam direction. A large impact parameter indicates that a particle has been produced in the decay of a parent body which was able to travel away from the interaction point before disintegrating. More information about the whole issue can be found in this series of posts, or by just clicking the “anomalous muons” tab in the column on the right of this text.
There are many things to say, but I will not say them all here now, because I am still digesting the presentation, the accompanying document produced by DZERO (not ready for public consumption yet), and the implications and subtleties involved. However, let me flash a few of the questions I am going to try and give an answer to with my readings:
- The paper does not address the most important question – what is DZERO’s track reconstruction efficiency as a function of track impact parameter ? They do discuss with some detail the complicated mixture of their data, which results from triggers which enforce that tracks have very small impact parameter -effectively cutting away all tracks with an impact parameter larger than 0.5cm- and a dedicated trigger which does not enforce an IP requirement; they also discuss their offline track reconstruction algorithms. But at a first sight it did not seem clear to me that they can actually reconstruct effectively tracks with impact parameters up to 2.5 cm as they claim. I would have inserted in the documents an efficiency graph for the reconstruction efficiency as a function of impact parameter, had I authored it.
- The paper shows a distribution of the decay radius of neutral K mesons, reconstructed from their decay into pair of charged pions. From the plot, the efficiency of reconstructing those pions is excessively small -some three times smaller than what it is in CMS, for instance. I need to read another paper by DZERO to figure out what drives their K-zero reconstruction efficiency to be so small, and whether this is in fact due to the decrease of effectiveness with track displacement.
- What really puzzles me, however, is the fact that they do not see *any* excess, while we know there must be in any case a significant one: decays in flight of charged kaons and pions. Why is it that CDF is riddled with those, while DZERO appears free of them ? To explain this point: charged kaons and pions yield muons, which get reconstructed as real muons with large impact parameter. If the decay occurs within the tracking volume, the track is partly reconstructed with the muon hits and partly with the kaon or pion hits. Now, while pions have a mass similar to that of muons, and thus the muon practically follows the pion trajectory faithfully, for kaons there must be a significant kink in the track trajectory. One expects that the track reconstruction algorithm will fail to associate inner hits to a good fraction of those tracks, and the resulting muons will belong to the “loose” category, without a correspondence in the “tight” muon category which has muons containing a silicon hit in the innermost layer of the silicon detector. This creates an excess of muons with large impact parameter. CDF does estimate that contribution, and it is quite large, of the order of tens of thousands of events in 743 inverse picobarns of data! Now where are those events in the DZERO dataset, then ?
Of course, you should not expect that my limited intellectual capabilities and my slow reading of a paper I have had in my hands for no longer than two hours can produce foulproof arguments. So the above is just a first pass, sort of a quick and dirty evaluation. I imagine I will be able to give an answer to those puzzles myself, at least in part, with a deeper look at the documentation. But, for the time being, this is what I have to say about the DZERO analysis.
Or rather, I should add something. By reading the above, you might get the impression that I am only criticizing DZERO out of bitterness for the failed discovery of the century by CDF… No, it is not the case: I have always thought, and I continue to think, that the multi-muon signal by CDF is some unaccounted-for background. And I do salute with relief and interest the new effort by DZERO on this issue. I actually thank them for providing their input on this mystery. However, I still retain some scepticism with respect to the findings of their study. I hope that scepticism can be wiped off by some input – maybe some reader belonging to DZERO wants to shed some light on the issues I mentioned above ? You are most welcome to do so!
UPDATE: Lubos pitches in, and guess what, he blames CDF… But Lubos the experimentalist is not better than Lubos the diplomat, if you know what I mean…
Other reactions will be collected below – if you have any to point to, please do so.
Some notes on the multi-muon analysis – part IV February 2, 2009
Posted by dorigo in news, physics, science.Tags: anomalous muons, CDF, new physics
comments closed
In this post -the fourth of a series (previous parts: part I, part II, and part III)- I wish to discuss a couple of attributes possessed by the “ghost” events unearthed by the CDF multi-muon analysis. A few months have passed since the publication of the CDF preprint describing that result, so I think it is useful for me to make a short summary below, repeating in a nutshell what is the signal we are discussing and how it came about.
Let me first of all remind you that “ghost events” are a unknown background component of the sample dimuon events collected by CDF. This background can be defined as an excess of events where one or both muons fail a standard selection criterion based on the pattern of hits left by the muons in the innermost layers of the silicon tracker, SVX. I feel I need to open a parenthesis here, in order to allow those of you who are unfamiliar with the detection of charged tracks to follow the discussion.
Two words on tracks and their quality
 The silicon tracker of CDF, SVX, is made up by seven concentrical cylinders of solid-state sensors (see figure on the right: SVX in Run II is made by the innermost L00 layer in red, plus four blue SVX II layers, plus two ISL layers; also shown are the two innermost Run I SVX’ layers, in hatched green), surrounding the beam line. When electrically charged particles created in a proton-antiproton collision travel out of the interaction region lying at the center, they cross those sensors in succession, leaving in each a localized ionization signal -a “hit”.
The silicon tracker of CDF, SVX, is made up by seven concentrical cylinders of solid-state sensors (see figure on the right: SVX in Run II is made by the innermost L00 layer in red, plus four blue SVX II layers, plus two ISL layers; also shown are the two innermost Run I SVX’ layers, in hatched green), surrounding the beam line. When electrically charged particles created in a proton-antiproton collision travel out of the interaction region lying at the center, they cross those sensors in succession, leaving in each a localized ionization signal -a “hit”.
CDF does not strictly need silicon hits to track charged particles, since outside of the silicon detector lies a gas tracker called COT (for Central Outer Tracker), capable of acquiring up to 96 additional independent position measurements of the ionization trail; however, silicon hits are a hundred times more precise than COT ones, so that one can define two different categories of tracks: COT-only, and SVX tracks. Only the latter are used for lifetime measurements of long-lived particles such as B hadrons, since those particles travel at most a few millimeters away from the primary interaction point before disintegrating: their decay products, if tracked with the silicon, allow the decay point to be determined.
Typically, CDF loosely requires an SVX track to have three or more hits; however, a tighter selection can be made which requires four or more hits, additionally enforcing that two of those belong to the two innermost silicon layers. These tight SVX tracks have considerably better spatial resolution on the point of origin of the track, since the two innermost hits “zoom in” on it very effectively.
Back to ghosts: a reminder of their definition
Getting back to ghost events, the whole evidence of their presence is that one finds considerably more muon pairs failing the tight-SVX tracking selection than geometry and kinematics would normally imply in a homogeneous sample of data. Muons in ghost events systematically fail hitting the innermost silicon layers, just as if they were produced outside of it by the decay of a long-lived, neutral particle.
Because of its very nature -an excess of muon pairs failing the tight-SVX criteria- the “ghost sample” is obtained by a subtraction procedure: one takes the number of events with a pair of tight-SVX muons, divides their number by the geometrical and kinematical efficiency
that muons from the various known sources pass tight-SVX cuts, and obtains a number
, which subtracted from the number
of observed dimuon pairs allows to spot the excess G, as follows:
.
Mind you, we are not talking of a small excess here: if you have been around this blog for long enough, you are probably accustomed to the frequent phenomenon of particle physicists getting hyped up for 10-event excesses. Not this time: the number of ghost muon events exceeds 70,000, and the nature of this contribution is clearly of systematic origin. It may be a background unaccounted by the subtraction procedure, or a signal involving muons that are created outside of the innermost silicon layers.
In the former three installments of this multi-threaded post I have discussed with some detail the significant sources of reconstructed muons which may contribute to the ghost sample, and be unaccounted by the subtraction procedure: muons from decays in flight of kaons and pions, fake muon tracks due to hadrons punching through the calorimeter, and secondary nuclear interactions. Today, I will rather assume that the excess of dimuon events constitutes a class of its own, different from those mundane sources, and proceed to discuss a couple of additional characteristics that make these events really peculiar.
The number of muons
 In the first part of this series I have discussed in detail how the excess of ghost events contains muons which have abnormally large impact parameters. Impact parameter -the distance of the track from the proton-antiproton collision point, as shown by the graph on the right- is a measure of the lifetime of the body which decays into the muons, and the observation of large impact parameters in ghost events is the real alarm bell, demanding that one needs to really try and figure out what is going on in the data. However, once that anomaly is acknowledged, surprises are not over.
In the first part of this series I have discussed in detail how the excess of ghost events contains muons which have abnormally large impact parameters. Impact parameter -the distance of the track from the proton-antiproton collision point, as shown by the graph on the right- is a measure of the lifetime of the body which decays into the muons, and the observation of large impact parameters in ghost events is the real alarm bell, demanding that one needs to really try and figure out what is going on in the data. However, once that anomaly is acknowledged, surprises are not over.
The second observation that makes one jump on the chair occurs when one simply counts the number of additional muon candidates found accompanying the duo which triggered the event collection in the first place. In the sample of 743,000 events with no SVX hit requirements on the two triggering muons, 72,000 events are found to contain at least a third muon track. 10% is a large number! By comparison, only 0.9% of the well-identified decays contained in the sample is found to contain additional muons besides the decay pair. However, since the production of
particles is a quite peculiar process, this observation need not worry us yet: those events are typically very clean, with the
meson accompanied by a relatively small energy release. In particle physics jargon, we say that
mesons have a soft
spectrum: they are produced almost at rest in most cases. There are thus few particles recoiling against it -and so, few muons too.
Now, the 10% number quoted above is not an accurate estimate of the fraction of ghost events containing additional muons, since it is extracted from the total sample -the 743,000 events. The subtraction procedure described above allows to estimate the fraction in the ghost sample alone: this is actually larger, 15.8%, because all other sources contribute fewer multi-muon events: only 8.3%. These fractions include of course both real and fake muons: in the following I try to describe how one can size up better those contributions.
Fake muons
A detailed account of the number of additional muons in the data and the relative sources that may be originating them can be tried by using a complete Monte Carlo simulation of all processes contributing to the sample, applying some corrections where needed. As a matter of fact, a detailed accounting of all the physical processes produced in proton-antiproton collisions is rather an overkill, because events with three or more muon candidates are a rare merchandise, and they can be produced by few processes: basically the only sizable contributions come from sequential heavy flavor decays and fake muon sources. Let us discuss these two possibilities in turn.
 Real muon pairs of small invariant mass, recoiling against a third muon, are usually the result of sequential decays of B-hadrons, like in the process
Real muon pairs of small invariant mass, recoiling against a third muon, are usually the result of sequential decays of B-hadrons, like in the process (see picture on the left, where the line of the decaying quark is shown emitting sequentially two lepton pairs in the weak decays). The two muons from such a chain decay cannot have a combined mass larger than 5 GeV, which is (roughly speaking) the mass of the originating B hadron. In fact, by enforcing that very requirement (
) on the two muons at trigger level, CDF enriches the collected dataset of events where two independent heavy-flavor hadrons (B or D mesons, for instance) are produced at a sizable angle from each other. A sample event picture is shown below in a transverse section of the CDF detector. Muon detection systems are shown in green, and in red are shown the track segments of two muons firing the high-mass dimuon trigger.

(You might well ask: Why does CDF requires a high mass for muon pairs ? Because the measurements that can be extracted from such a “high-mass” sample are more interesting than those granted by events with two muons produced close in angle, events which are in any case likely to be collected into different datasets, such as the one triggered by a single muon with a larger transverse momentum threshold. But that is a detail, so let’s go back to ghost muons now.)
When there are three real muons, one thus has most likely a $b \bar b$ pair, with one of the quarks producing a double semileptonic decay (two muons of small mass and angle), and the other producing a single semileptonic decay (with this third muon making a large mass with one of the other two): for instance, , in the case of two B mesons; in the decay chain above, X and Y denote a generic hadronic state, while D is a hadron containing a anti-charm quark. B hadron decays can produce three muons also when one of them decays to a
meson, which in turn decays to a muon pair. Other heavy flavor decays, like those involving a
pair, can at most produce a pair of muons, and the third one must then be a fake one.
The HERWIG Monte Carlo program, which simulates all QCD processes, does make a good guess of the production cross-section of b-quark pairs and c-quark pairs produced in proton-antiproton collisions, in order to simulate all processes with equanimity; but those numbers are not accurate. One improves things by taking simulated events that contain those production processes such that they match the and
cross-sections which are measured with the tight-SVX sample, the subset devoid of the ghost contribution.
The CDF analysis then proceeds by estimating the number of events where at least one muon track is in reality a hadron which punched through the detector. The simulation can be trusted to reproduce the number of hadrons and their momentum spectrum, but the phenomenon of punch-through is unknown to it! To include it, a parametrization of the punch-through probability is obtained from a large sample of decays, collected by the Silicon Vertex Tracker, a wonderful device capable of triggering on the impact parameter of tracks. The
meson lives long enough that the kaon and pion tracks it produces have sizable impact parameter, and millions of such events have been collected by CDF in Run II.
The extraction of the probability is quite simple: take the kaon tracks from D decays, and find the fraction of these tracks that are considered muon candidates, thanks to muon chamber hits consistent with their trajectory. Then, repeat the same with the pion candidates. The result is shown in the graphs below separately for kaon and pion tracks. In them, the probability has been computed as a function of the track transverse momentum.

Besides the above probabilities and the tuning of the cross section, a number of other details are needed to produce a best-guess prediction of the number of multi-mion events with the HERWIG Monte Carlo simulation. However, once all is said and done, one can verify that there indeed is an excess in the data. This excess appears entirely in the ghost muon sample, while the tight-SVX sample is completely free from it. Its size is again very large, and its source is thus systematical -no fluctuation can be hypothesized to have originated it.
The mass of muon pairs in multi-muon events
To summarize, what happens with ghost events is that if one searches for additional muon tracks around each of the triggering muons, one finds them with a rate much higher than what one observes in the tight-SVX dimuon sample. It is as if a congregation of muons is occurring! The standard model is unable to even getting close to explain how events with so many muons can be produced. The source of ghost events is thus really mysterious.
Now, if you give to a particle physicist the momenta and energies of two particles produced together in a mysterious process, there is no question on what is going to happen: next thing you know, he will produce a number,
.
is the invariant mass of the two-particle system: if they are the sole products of a decay process, m is a unbiased measurement of the mass
of the parent body. If, instead, the two particles are only part of the final state, m will be smaller than
; still, a distribution of the quantity m for several decays will say a lot about the parent particle X.
Given the above, it is not a surprise that the next step in the analysis, once triggering muons in ghost events are found to be accompanied by additional muons at an abnormal rate, is to plot the invariant mass of those two-muon combinations.
 There is, however, an even stronger motivation from doing that: an anomalous mass distribution of lepton pairs (then electron-muon pairs, not dimuons -I will come back to this detail later) had been observed by the same authors in Run I. That excess of dilepton pairs was smaller numerically -the dataset from which it had been extracted corresponded to an integrated luminosity 20 times smaller- but had been extracted with quite different means, from a different trigger, and with a considerably different detector (the tracking of CDF has been entirely changed in Run II). The low-mass excess of dilepton pairs remained a unexplained feature, calling for more investigation which had to wait a few years to be performed. The mass distribution of electron-muon combinations found by CDF in Run I is shown in the graph on the right: the excess of data (the blue points) over known background sources (the yellow histogram) appears at very low mass.
There is, however, an even stronger motivation from doing that: an anomalous mass distribution of lepton pairs (then electron-muon pairs, not dimuons -I will come back to this detail later) had been observed by the same authors in Run I. That excess of dilepton pairs was smaller numerically -the dataset from which it had been extracted corresponded to an integrated luminosity 20 times smaller- but had been extracted with quite different means, from a different trigger, and with a considerably different detector (the tracking of CDF has been entirely changed in Run II). The low-mass excess of dilepton pairs remained a unexplained feature, calling for more investigation which had to wait a few years to be performed. The mass distribution of electron-muon combinations found by CDF in Run I is shown in the graph on the right: the excess of data (the blue points) over known background sources (the yellow histogram) appears at very low mass.
In Run II, not only does CDF have 20 times more data (well, sixty times so by now, but the dataset on which this analysis was performed was frozen one and a half years ago, thus missing the data collected and processed after that date): we also have more tools at our disposal. The mass distribution of muon pairs close in angle, belonging to ghost events with three or more muon candidates, can be compared with the tuned HERWIG simulation both for ghost event sample and for the tight SVX sample: this makes for a wonderful cross-check that the simulation can be trusted on producing a sound estimate of that distribution!
 The invariant mass distribution of muon pairs close in angle in tight-SVX events with three or more muon tracks is shown on the left. The experimental data is shown with full black dots, while the Monte Carlo simulation prediction is shown with empty ones. The shape and size of the two distributions match well, implying that the Monte Carlo is properly normalized. Indeed, the tight-SVX sample is the one used for the measurements of
The invariant mass distribution of muon pairs close in angle in tight-SVX events with three or more muon tracks is shown on the left. The experimental data is shown with full black dots, while the Monte Carlo simulation prediction is shown with empty ones. The shape and size of the two distributions match well, implying that the Monte Carlo is properly normalized. Indeed, the tight-SVX sample is the one used for the measurements of and
cross sections: once the Monte Carlo is tuned to the values extracted from the data, its overall normalization could mismatch the data only if fake-muon sources were grossly mistaken. That is not the case, and further, one observes that the number of
decays -which end up all in one bin in the histogram, at 3.1 GeV of mass- are perfectly well predicted by the simulation: again, not a surprise, since those mesons can make it to a three-muon dataset virtually only if they are originated from B hadron decays. So, the check in tight-SVX events fortifies our trust on our tuned Monte Carlo tool.
 Now, let us look at how things are going in the ghost muon sample (see graph on the right). Here, we observe more data at low invariant mass than what the Monte Carlo predicts: there is a clear excess for masses below 2.5 GeV. This excess has the same shape as the one observed in Run I in electron-muon combinations!
Now, let us look at how things are going in the ghost muon sample (see graph on the right). Here, we observe more data at low invariant mass than what the Monte Carlo predicts: there is a clear excess for masses below 2.5 GeV. This excess has the same shape as the one observed in Run I in electron-muon combinations!
Please take a moment to record this: in CDF, some of the collaborators who objected to the publication of the multi-muon analysis did so because they insisted that more studies should be made to confirm or disprove the effect. One of the objections was that the electron-muon sample had not been studied yet. The rationale is that if the ghost events are due to a real physical process, then the same process should show up in electron-muon combinations; otherwise, one is hard-pressed to avoid having to put into question a thing called lepton universality, which -at least for Standard Model processes- is a really hard thing to do. However, the electron signature in CDF is very difficult to handle, particularly at low energy: backgrounds are much harder to pinpoint than for muons. Such a study is ongoing, but it might take a long time to complete. Run I, instead, is there for us: and there, the same excess was indeed present in electron events too!
Finally, there is one additional point to mention: a small, but crucial one. The signal is in perfect match with the simulation prediction! This observation confirms that the tuned cross section of
production is right dead-on. Whatever these ghost events are, they sure cannot be coming from B production. Also, note that the agreement of the
signal with Monte Carlo expectations constitutes proof that the efficiency of the tight-SVX requirements -the 24% number which is used to extract the numerical excess of ghost events- is correct. Everything points to a mysterious contribution which is absent in the Monte Carlo.
The above observations conclude this part of the discussion. In the next installment, I will try to discuss the additional oddities of ghost events -in particular, the rate of muons exceeding the triggering pair is actually four times higher than in QCD events. I will then examine some tentative interpretations that have been put forth in the course of the three months that have passed since the publication.
Multi-muon news January 26, 2009
Posted by dorigo in news, personal, physics, science.Tags: anomalous muons, CDF, CMS, D0, new physics
comments closed
This post is not it but no, I have not given up on my promise to complete my series on the anomalous multi-muon signal found by CDF in its Run II data. In fact, I expect to be able to post once more on the topic this week. There, I hope I will be able to discuss the kinematic characteristics of multi-lepton jets. [I am lazy today, so I will refrain from adding links to past discussions of the topic here: if you need references on the topic, just click on the tag cloud on the right column, where it says “anomalous muons“!]
In the meantime, I am happy to report that I have just started working at the same analysis for the CMS experiment! In Padova we have recently put together a group of six -one professor, three researchers, a PhD student, and a undergrad- and we will pursue the investigation of the same signature seen by CDF. And today, together with Luca, our new brilliant PhD student, I started looking at the reconstruction of neutral kaon decays , a clean source of well-identified pion tracks with which we hope to be able to study muon mis-identification in CMS.
Meanwhile, the six-strong group in Padova is already expanding. Last Wednesday professor Fotios Ptochos, a longtime colleague in CDF, a good friend, and crucially one of the authors of the multi-muon analysis, came to Padova and presented a two-hour-long seminar on the CDF signal in front of a very interested group of forty physicists spanning four generations -from Milla Baldo Ceolin to our youngest undergraduates. The seminar was enlightening and I was very happy with the result of a week spent organizing the whole thing! (I will have to ask Fotios if I can make the slides of his talk available here….)
Fotios, a professor at the University of Cyprus, is a member of CMS, and a true expert of measurements in the B-physics sector at hadron machines. We plan to work together to repeat the controversial CDF analysis with the first data that CMS will collect -hopefully later this year.
The idea of repeating the CDF analysis in CMS is obvious. Both CDF and D0 can say something on the signal in a reasonable time scale, but whatever the outcome, the matter will only be settled by the LHC experiments. Imagine, for instance, that in a few months D0 publishes an analysis which disproves the CDF signal. Will we then conclude that CDF has completely screwed up its measurement ? We will probably have quite a clue in that case, but we will need to remain possibilistic until at least a third, possibly more precise, measurement is performed by an independent experiment.That measurement is surely going to be worth a useful publication.
And now imagine, on the contrary, that the CDF signal is real…
No CHAMPS in CDF data January 12, 2009
Posted by dorigo in news, physics, science.Tags: CDF, Champ, dark matter, new physics, SUSY
comments closed
A recent search for long-lived charged massive particles in CDF data has found no signal in 1.0 inverse femtobarns of proton-antiproton collisions produced by the Tevatron collider at Fermilab.
Most subnuclear particles we know have very short lifetimes: they disintegrate into lighter bodies by the action of strong, or electromagnetic, or weak interactions. In the first case the particle is by necessity a hadron- one composed of quarks and gluons-, and the strength of the interaction that disintegrates it is evident by the fact that the life of the particle is extremely short: we are talking about a billionth of a trillionth of a second, or even less time. In the second case, the electromagnetic decay takes longer, but still in most instances a ridiculously small time; the neutral pion, for instance, decays to two photons () in about
seconds: eighty billionths of a billionth of a second. In the third case, however, the weakness of the interaction manifests itself in decay times that are typically long enough that the particle is indeed capable of traveling for a while.
Currently, the longest-living subnuclear particle is the neutron, which lives about 15 minutes before undergoing the weak decay , the well-studied beta-decay process which is at the basis of a host of radioactive phenomena. The neutron is very lucky, however, because its long life is not only due to the weakness of virtual W-boson exchange, but also by the fact that this particle happens to have a mass just a tiny bit larger than the sum of the bodies it must decay into: this translates in a very, very small “phase space” for the decay products, and a small phase space means a small decay rate.
Of course, we have only discussed unstable particles so far: but the landscape of particle physics includes also stable particles, i.e. the proton, the electron, the photon, and (as far as we know) the neutrinos. We would be very surprised if this latter set included particles we have not discovered yet, but we should be more possibilistic.
A stable, electrically-neutral massive particle would be less easy to detect than we could naively think. In fact, most dark-matter searches aimed at detecting a signal of a stable massive particle are tuned to be sensitive to very small signals: if a gas of neutralinos pervaded the universe, we might be unaware of their presence until we looked at rotation curves of galaxies and other non-trivial data, and even then, a direct signal in a detector would require extremely good sensitivity, since a stable neutral particle would be typically very weakly interacting, which means that swarms of such bodies could easily fly through whatever detector we cook up unscathed. Despite that, we of course are looking for such things, with CDMS, DAMA, and other dark-matter-dedicated experiments.
The existence of a charged massive stable particle (CHAMP for friends), however, is harder to buy. An electrically-charged particle does not go unseen for long: its electromagnetic interaction is liable to betray it easily. However, there is no need to require that a CHAMP is by force THE reason of missing mass in the universe. These particles could be rare, or even non-existent in the Universe today, and in that case our only chance to see them would be in hadron-collision experiments, where we could produce them if the energy and collision rate are sufficient.
What would happen in the event of a creation of a CHAMP in a hadron collision is that the particle would slowly traverse the detector, leaving a ionization trail. A weak-interacting CHAMP (and to some extent even a strongly-interacting one) would not interact strongly with the heavy layers of iron and lead making up the calorimeter systems of which collider experiments are equipped, and so it would be able to punch through, leaving a signal in the muon chambers before drifting away. What we could see, if we looked carefully, would be a muon track which ionizes the gas much more than muons usually do -because massive CHAMPS are heavy, and so they kick atoms around as they traverse the gas. Also, the low velocity of the particle (be it clear, here “low” means “only few tenths of the speed of light”!) would manifest itself in a delay in the detector signals as the particle traverses them in succession.
CDF has searched for such evidence in its data, by selecting muon candidates and determining whether their crossing time and ionization is compatible with muon tracks or not. More specifically, by directly measuring the time needed for the track to cross the 1.5 meter-radius of the inner tracker, and the particle momentum, the mass of the particle can be inferred. That is easier said than done, however: a muon takes about 5 nanoseconds to traverse the 1.5 meters of the tracker, and to discern a particle moving half that fast, one is requred to measure this time interval with a resolution better than a couple of nanoseconds.
The CDF Time-Of-Flight system (TOF) is capable of doing that. One just needs to determine the production time with enough precision, and then the scintillation bars which are mounted just outside of the tracking chamber (the COT, for central outer tracker) will measure the time delay. The problem with this technique, however, is that the time resolution has a distinctly non-Gaussian behaviour, which may introduce large backgrounds when one selects tracks compatible with a long travel time. The redundancy of CDF comes to the rescue: one can measure the travel time of the particles through the tracker by looking at the residuals of the track fit. Let me explain.
A charged particle crossing the COT leaves a ionization trail. These ions are detected by 96 planes of sense wires along the path, and from the pattern of hit wires the trajectory can be reconstructed. However, each wire will have recorded the released charge at a different time, because they are located at different distances from the track, and the ions take some time to drift in the electric field before their signal is collected. The hit time is used in the fit that determines the particle trajectory: residuals of these time measurements after the track is fit provide a measurement of the particle velocity. In fact, a particle moving slowly creates ionization signals that are progressively delayed as a function of radius; these residuals can be used to determine the travel time.
The resulting measurement has a three-times-worse precision than that coming from the dedicated TOF system (fortunately, I would say, otherwise the TOF itself would be a rather useless tool); however, the uncertainty on this latter measurement has a much more Gaussian behaviour! This is an important asset, since by requiring that the two time measurements are consistent with one another, one can effectively remove the non-Gaussian behavior of the TOF measurement.
By combining crossing time -i.e. velocity- and track momentum measurement, one may then derive a mass estimate for the particle. The distribution of reconstructed masses for CHAMP candidates is shown in the graph below. Overimposed to the data, the distribution expected for a 220-GeV CHAMP signal has been overlaid. It is clear to see that the mass resolution provided by the method is rather poor: despite of that, a high-mass charged particle would be easy to spot if it were there.
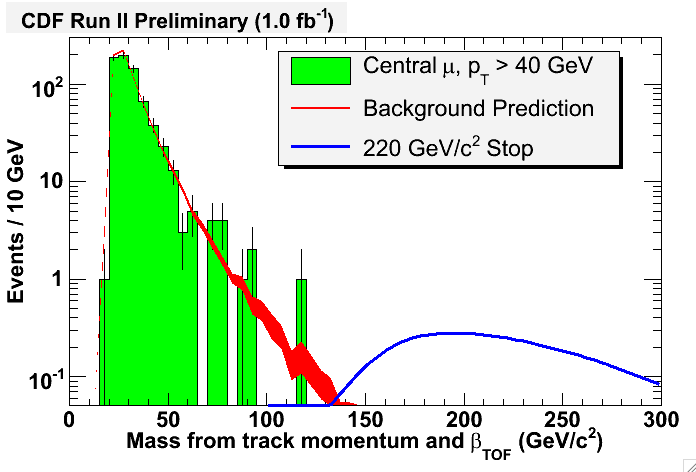
One note of warning about this graph: the distribution above shows masses ranging all the way from 0 to 100 GeV, but that does not mean that these tracks have similar masses: the vast majority of tracks are real muons, for which the velocity is underestimated due to instrumental effects: in a sense, the very shape of the curve describes the resolution of the time measurement provided by the analysis.
The absence of tracks compatible with a mass larger than 120 GeV in the data allows to place model-independent limits on the CHAMP mass. Weak-interacting CHAMPS are excluded, in the kinematic region covered by the muon chambers, and with
, if they are produced with a cross section larger than 10 fb. For strongly-interacting CHAMPS the search considers the case of a scalar top R-hadron, a particle which is predicted by Supersymmetric theories when the stable stop quark binds together with an ordinary quark. In that case, the 95% CL limit can be set at a mass of 249 GeV.
It is interesting to note that this analysis, while not using the magnitude of the ionization left by the track in the gas chamber (the so-called on which most past searches of CHAMPS have been based, e.g. in CDF (Run I) and ALEPH) to identify the CHAMP signal candidates, still does use the
to infer the (background) particle species when determining the resolution of the time measurement from COT residuals. So the measurement shows once more how collider detectors really benefit from the high redundancy of their design!
[Post scriptum: I discuss in simple terms the ionization energy loss in the second half of this recent post.]
It only remains to congratulate with the main authors of this search, Thomas Phillips (from Duke University) and Rick Snider (Fermilab), for their nice result, which is being sent for publication as we speak. The public web page of the analysis, which contains more plots and an abstract, can be browsed here.
Some posts you might have missed in 2008 – part II January 6, 2009
Posted by dorigo in physics, science.Tags: anomalous muons, CDF, D0, Higgs boson, LHC, Lubos Motl, new physics, PDF, QCD, Tevatron, top mass, top quark, Z boson
comments closed
Here is the second part of the list of useful physics posts I published on this site in 2008. As noted yesterday when I published the list for the first six months of 2008, this list does not include guest posts nor conference reports, which may be valuable but belong to a different place (and are linked from permanent pages above). In reverse chronological order:
December 29: a report on the first measurement of exclusive production of charmonium states in hadron-hadron collisions, by CDF.
December 19: a detailed description of the effects of parton distribution functions on the production of Z bosons at the LHC, and how these effects determine the observed mass of the produced Z bosons. On the same topic, there is a maybe simpler post from November 25th.
December 8: description of a new technique to measure the top quark mass in dileptonic decays by CDF.
November 28: a report on the measurement of extremely rare decays of B hadrons, and their implications.
November 19, November 20, November 20 again , November 21, and November 21 again: a five-post saga on the disagreement between Lubos Motl and yours truly on a detail on the multi-muon analysis by CDF, which becomes a endless diatriba since Lubos won’t listen to my attempts at making his brain work, and insists on his mistake. This leads to a back-and-forth between our blogs and a surprising happy ending when Motl finally apologizes for his mistake. Stuff for expert lubologists, but I could not help adding the above links to this summary. Beware, most of the fun is in the comments threads!
November 8, November 8 again, and November 12: a three-part discussion of the details in the surprising new measurement of anomalous multi-muon production published by CDF (whose summary is here). Warning: I intend to continue this series as I find the time, to complete the detailed description of this potentially groundbreaking study.
October 24: the analysis by which D0 extracts evidence for diboson production using the dilepton plus dijet final state, a difficult, background-ridden signature. The same search, performed by CDF, is reported in detail in a post published on October 13.
September 23: a description of an automated global search for new physics in CDF data, and its intriguing results.
September 19: the discovery of the baryon, an important find by the D0 experiment.
August 27: a report on the D0 measurement of the polarization of Upsilon mesons -states made up by a pair- and its relevance for our understanding of QCD.
August 21: a detailed discussion of the ingredients necessary to measure with the utmost precision the mass of the W boson at the Tevatron.
August 8: the new CDF measurement of the lifetime of the baryon, which had previously been in disagreement with theory.
August 7: a discussion of the new cross-section limits on Higgs boson production, and the first exclusion of the 170 GeV mass, by the two Tevatron experiments.
July 18: a search for narrow resonances decaying to muon pairs in CDF data excludes the tentative signal seen by CDF in Run I.
July 10: An important measurement by CDF on the correlated production of pairs of b-quark jets. This measurement is a cornerstone of the observation of anomalous multi-muon events that CDF published at the end of October 2008 (see above).
July 8: a report of a new technique to measure the top quark mass which is very important for the LHC, and the results obtained on CDF data. For a similar technique of relevance to LHC, also check this other CDF measurement.
Some posts you might have missed in 2008 January 5, 2009
Posted by dorigo in cosmology, personal, physics, science.Tags: CDF, CMS, dark matter, Higgs boson, LHC, new physics, particle detectors, physics, standard model, SUSY, top quark, top quark mass
comments closed
To start 2009 with a tidy desk, I wish to put some order in the posts about particle physics I wrote in 2008. By collecting a few links here, I save from oblivion the most meaningful of them -or at least I make them just a bit more accessible. In due time, I will update the “physics made easy” page, but that is work for another free day.
The list below collects in reverse chronological order the posts from the first six months of 2008; tomorrow I will complete the list with the second half of the year. The list does not include guest posts nor conference reports, which may be valuable but belong to a different list (and are linked from permanent pages above).
June 17: A description of a general search performed by CDF for events featuring photons and missing transverse energy along with b-quark jets – a signature which may arise from new physics processes.
June 6: This post reports on the observation of the decay of J/Psi mesons to three photons, a rare and beautiful signature found by CLEO-c.
June 4 and June 5 offer a riddle from a simple measurement of the muon lifetime. Readers are given a description of the experimental apparatus, and they have to figure out what they should expect as the result of the experiment.
May 29: A detailed discussion of the search performed by CDF for a MSSM Higgs boson in the two-tau-lepton decay. Since this final state provided a 2.1-sigma excess in 2007, the topic deserved a careful look, which is provided in the post.
May 20: Commented slides of my talk at PPC 2008, on new results from the CDF experiment.
May 17: A description of the search for dimuon decays of the B mesons in CDF, which provides exclusion limits for a chunk of SUSY parameter space.
May 02 : A description of the search for Higgs bosons in the 4-jet final state, which is dear to me because I worked at that signature in the past.
Apr 29: This post describes the method I am working on to correct the measurement of charged track momenta by the CMS detector.
Apr 23, Apr 28, and May 6: This is a lengthy but simple, general discussion of dark matter searches with hadron colliders, based on a seminar I gave to undergraduate students in Padova. In three parts.
Apr 6 and Apr 11: a detailed two-part description of the detectors of electromagnetic and hadronic showers, and the related physics.
Apr 05: a general discussion of the detectors for LHC and the reasons they are built the way they are.
Mar 29: A discussion of the recent Tevatron results on Higgs boson searches, with some considerations on the chances for the consistence of a light Higgs boson with the available data.
Mar 25: A detailed discussion on the possibility that more than three families of elementary fermions exist, and a description of the latest search by CDF for a fourth-generation quark.
Mar 17: A discussion of the excess of events featuring leptons of the same electric charge, seen by CDF and evidenced by a global search for new physics. Can be read alone or in combination with the former post on the same subject.
Mar 10: This is a discussion of the many measurements obtained by CDF and D0 on the top-quark mass, and their combination, which involves a few subtleties.
Mar 5: This is a discussion of the CDMS dark matter search results, and the implications for Supersymmetry and its parameter space.
Feb 19: This is a divulgative description of the ways by which the proton structure can be studied in hadron collisions, studying the parton distribution functions and how these affect the scattering measurements in proton-antiproton collisions.
Feb 13: A discussion of luminosity, cross sections, and rate of collisions at the LHC, with some easy calculations of the rate of multiple hard interactions.
Jan 31: A summary of the enlightening review talk on the standard model that Guido Altarelli gave in Perugia at a meeting of the italian LHC community.
Jan 13: commented slides of the paper seminar gave by Julien Donini on the measurement of the b-jet energy scale and the cross section, the latter measured for the first time ever at a hadron machine. This is the culmination of a twelve-year effort by me and my group.
Jan 4: An account of the CDF search for Randall-Sundrum gravitons in the final state.
Scientific wishes for 2009 December 31, 2008
Posted by dorigo in astronomy, Blogroll, cosmology, personal, physics, science.Tags: anomalous muons, LHC, new physics, standard model
comments closed
I wish 2009 will bring an answer to a few important questions:
- Can LHC run ?
- Can LHC run at 14 TeV ?
- Will I get tenure ?
- Are multi-muons a background ?
- Are the Pamela/ATIC signals a prologue of a new scientific revolution ?
- Will England allow a NZ scientist to work on Category Theory on its soil ?
- Is the Standard Model still alive and kicking in the face of several recent attempts at its demise ?
I believe the answer to all the above questions is yes. However, I am by no means sure all of them will be answered next year.
A few remarks on Matthew Strassler’s “Flesh and Blood with Multi-Muons” November 17, 2008
Posted by dorigo in news, physics, science.Tags: anomalous muons, arxiv, CDF, new physics
comments closed
[I know, I know… I had promised that today I would issue a fourth installment of my multi-threaded post on the multi-muon analysis, and instead this morning (well, that depends where you’re sitting) I am offering you something slightly different: instead than concrete details on the analysis, here is a review of a review of the same. I trust you understand that blogs, like newspapers or magazines, have their own priority lists…]
Last evening I read with a mixture of interest and surprise the paper recently appeared on the Arxiv by Matthew Strassler, a theorist from Rutgers University, and a supporter of so-called “hidden valley” models of physics beyond the Standard Model.
The interest stems from obvious reasons: after CDF published the study on multi-muon events, any discussion of the effect, as much as any tentative explanation -be it a mundane or an exotic one- is worth my undivided attention. And, mind you, let me say from the outset that I salute professor Strassler’s thoughts and considerations as useful and stimulating, and the mechanisms he suggests promising avenues for further research on the subject.
But there’s room for surprise, and not all of it is of pleasant nature.
Some of the surprise comes from a few of the remarks contained in the 20-pages document, and some comes from the way it is written. More on the remarks below, while about the way it is written I can say off-hand that I should probably be grateful to theorists these days, since they have started to make their papers free of complicated formulas, at the expense of a rather large rate of unnecessary adjectives: Strassler’s paper has indeed a remarkable formula count of zero.
In general I feel surprised by reading in an Arxiv paper something one usually finds in a blog: a list of ideas and questions concerning a paper published by a respectable scientific collaboration. It looks like prof. Strassler does not have a blog, and so he uses the Arxiv as a dump of his train of thoughts. Incidentally, this blog is of course open to him for a guest post, if he ever wants to try this kind of arena for his ideas.
I guess my criticism on the style boils down to this: it seems less productive to write an Arxiv paper containing a list of ideas and questions -and quite a bit of criticism-, than just picking up the phone and call the authors of the analysis, as I am told many other theorists are doing these days. No, he apparently has not made the phone call yet. That is quite unfortunate, because if he had he would maybe have learned a thing or two about the CDF analysis beyond what is published, and he would have had a chance to find an answer to some of his questions. Then, his ideas might have gotten some useful input and could have been refined. In his paper, instead, they sometimes read like a laundry list (check for instance pages 18-19, where he has seven bullets of plots he asks CDF to produce).
In his preprint Strassler mentions repeatedly that the multi-muon paper is written by “a subset of the CDF collaboration“. It appears that he stresses this fact on purpose, as if it is a datum of scientific importance. Fortunately he does not go as far as to claim that his observation casts doubt on the results, but his lingering on the issue appears strange, and to me, inappropriate. Calling our publication “a paper by a subset of the CDF collaboration” is plain wrong, because the paper is by the CDF collaboration, regardless of who signs it. The collaboration is one, and it is more than a collection of individuals: it admits no subset. I know theorists are much more promiscuous in the way they associate and disperse in different author lists; but a collaboration is a collaboration, and once a member, you only get to decide whether to sign or not a paper, but the collaboration publishes, not you.
This matter is important, so maybe I need to stress it once more. Let me remind everybody that the multi-muon analysis is a CDF publication, and that the CDF collaboration stands by this paper just as much as it stands by every other one of the half thousand it has published in its long, illustrious life. Signing a CDF paper is a great privilege, and since prof. Strassler does not know personally all of the people in CDF (I, for one, never had the pleasure to meet him), nor does he know about the internal discussions that have taken place concerning the publication, he should be expected to leave this issue aside, lest he gives the impression of discussing matters he is wholly unqualified to discuss. This impression is set from the very beginning in Strassler’s preprint, and remains in the background throughout its 20 pages, resonating in a few specific spots.
Let me now go into the contents of the “flesh and blood” paper very briefly. I cannot discuss all of it here today, but I will make an attempt at showing a couple of further examples of what I do not like in it, thereby creating a biased view of my overall opinion: the parts I liked will be left out of this post. Also, in the process of showing what I object to, I will be quoting out of context: a rather reproachable conduct, I must admit, but I have no real choice if I want to make this post shorter than the paper it deals with.
So here is the very incipit of the Introduction:
“Very recently, an unknown subset of the CDF collaboration has signed its name to one of particle physics’ most extraordinary papers”.
Well, after thanking prof. Strassler for the unnecessary, improbable adjective, one is left wondering whether he can compute the ratio of small integers, like 370/600. But, at least until we get to read about his cross section estimates, we prefer to grant that he can, and so we have to hypothesize that maybe, by “unknown subset” he means to say he does not know the 370 authors who signed the “extraordinary paper”. Paraphrasing Oscar Wilde, “To not know an experimentalist is an accident; to not know 370 is carelessness“. But Strassler does know at least two CDF members: these are two of his Rutgers colleagues, who in fact get thanked in the concluding lines of his paper. Unfortunately, they did not sign the CDF publication. From this one might be tempted to speculate that Strassler only got to hear comments and internal information biased in a particular direction…
Yet prof. Strassler is quite clear to state from the outset he is very interested in the CDF analysis:
“No one would be happier than the author of the present note if this “suggestion of evidence” were to hold up under scrutiny”.
I omit discussing whether I find acceptable or not the way he interprets as a “suggestion of evidence” the conclusions of the CDF study, but I cannot fail to explain that he should rather take a ticket and join the line of happy scientists cheering the discovery of new physics, than single out himself as the one. This is a small bit of immodesty which however, after having noted it, I think we should pardon, given that he has indeed worked on hidden valley models for a long time.
We can also pardon him for saying that the paper is “too short given its potential importance“, right in the next paragraph. On this one count, I think he really manages to stand out of the crowd head and shoulders: of all the comments I have heard about the CDF paper, none went so far as to say that the 70 pages were too few.
Then, a sentence I am still trying to decypher:
“No serious attempt is made to interpret the data. This exercise may well be helpful […] even if the specific results of [1] (and a related attempt at an intepretation by the experimentalists involved [11]) are eventually discredited.”
Does Strassler mean to say that the study in [11] (the interpretation of multi-muon events, by the original authors of the study) was unserious ? Or does he rather mean it is useful to put together interpretations of similar effects even if they end up straight in the waste bin ? That would justify the career of a lot of theorists…
After the above sentences, which are contained in the introduction, we find section II, which is called “Preliminary comments“. Here I am puzzled to find Strassler’s paper wrestling with the number of events quoted in the CDF publication, reaching odd conclusions. Strassler incorrectly quotes 75 picobarns as the cross-section for ghost events: a number which comes out of the blue, and for which my explanation is the following: he uses the number of ghost events, “153895” as he quotes (forgetting this number refers to the subset of “ghost events” passing loose SVX criteria, but of that I can pardon him, he has a thing with subsets), and he assumes this corresponds to 2.1 inverse femtobarns of data. Then, would do the trick: 150k divided by 2k inverse picobarns is indeed 75 picobarns . Is this what he computed ? Well, it is wrong, since the luminosity corresponding to the 153,895 events is 742 inverse picobarns, and not 2.1/fb. See, this is one of the many instances when one cannot help noticing that a phone call before submitting to the Arxiv would have been a good idea. Cross section estimates are best left with experimentalists, otherwise what will we do for a living ?
Also odd is his following remark:
“if the efficiency estimate were in error for a subclass of events, and the efficiency were only, say, 23.4 percent, then the number of ghost events would drop by 1/5”.
Now, please. CDF publishes a paper, it quotes an efficiency (24.4+-0.2%), and it estimates an excess. What do we get if a theorist, albeit a distinguished one, ventures to say that if the efficiency were wrong (by 5-sigma from the quoted value), the excess would be significantly different ? I miss the scientific value of that sentence. Wait, there is more: only a paragraph below he insists:
“For these two reasons, we must view the number of unexplained ghost events as highly uncertain”.
Excuse me: we own the data, we publish an estimate, we give a uncertainty. You may well question whether it is correct or not, but simply saying an estimate is “highly uncertain” without coming down to explain what mechanisms may have caused an error in the CDF determination of the efficiency, is not constructive criticism, and is rather annoying. Not to mention that the CDF publication where the ingredients for the determination of that efficiency were measured is not quoted in Strassler’s paper!
Ok, I think I have done enough commenting for today. To conclude this post, I will quote without commentary a few sentences which I find peculiar. I have to say it: while the CDF paper is not the clearest I have had the pleasure to sign, I feel the need to stand by it when I see it attacked by non-constructive criticism.
- “…the paper[…] is far too short given its potential importance, and many critical plots that could support the case are absent”.
- “No serious attempt is made to interpret the data”.
- “It is not clear why these checks were not performed”.
- “There are a number of other plots whose presence, or absence, in Appendix B of [1] is very surprising. In particular, though obviously presented so as to support the interpretation of [11], the plots in Appendix B do not actually appear to do so.”
- “…the challenges that this analysis faces are useful as a springboard for discussion. Clearly, if there were a signal of this type in the data, it would indeed by quite difficult to find it, and the approach used in [1] is far from optimal.”
After this list of less-than-constructive comments, let me quote Freeman Dyson for a change:
“The professional duty of a scientist confronted with a new and exciting theory (or data) is to try to prove it wrong. That is the way science works. This is the way science stay honest. Criticism is absolutely necessary to make room for better understanding.”
Am I the only one to think Dyson meant constructive criticism ?
UPDATE: version 2 of Strassler’s paper came out on November 17th, a week after version 1. This new version makes no mention at all of the “subset” of CDF authors. I thank Matthew Strassler for realizing this correction was useful.
Some notes on the multi-muon analysis – part III November 12, 2008
Posted by dorigo in news, physics, science.Tags: anomalous muons, CDF, new physics
comments closed
This is the third part of a multi-part post (see part 1 and part 2) on the recent analysis sent to Phys.Rev.D by the CDF collaboration (including myself -I did sign the paper!) on their multi-muon signal, which might constitute the first evidence for new physics beyond the Standard Model -or the unearthing of a nagging background which has ridden several past CDF analyses, particularly in the B quark sector. I apologize with those of you who feel this post is above your head: the matter discussed is really, really complicated, and it would be almost impossible to make it accessible to everybody. I have made an attempt at simplifying some things, and summarizing each step of the discussion below, but I understand it might remain rather obscure to some of you. Sorry. My only way to repair is to make myself available to explain anything in more detail, at your request…
Today, I wish to discuss one additional source of background to the “ghost” sample, which -I remind you as well as myself- consists of an excess of events where the two triggering muons left no hits in the inner layers of the CDF silicon detector; this excess results from a subtraction of known sources of muon pairs from the original sample. Identified muon tracks in the ghost sample are measured to possess an abnormally large impact parameter (impact parameter is the minimum distance between backward-extrapolated track and collision point, in the plane transverse to the beam direction); the distribution of these impact parameters shows a long tail
suggestive of the decay in flight of a long-lived particle.
As I discussed earlier, there are in principle four different sources of such muons: real or fake muons, with either a well-measured, large impact parameter, or with an impact parameter
which is large because of a wrong reconstruction of the track. In the paper, these combinations are rather divided into the different physical processes that may give rise to such signatures:
- punch-through of light hadrons mimicking a muon signal, which are a source of fake muons with large impact parameter;
- misreconstructed muon tracks from B decays, which are a source of real muons for which impact parameter may be mismeasured;
- in-flight decays of light hadrons (
,
), which are a source of real muons with badly measured impact parameter;
- secondary nuclear interactions in the material contained in the tracker, which cause tracks to have a large impact parameter, and may in principle be a source of fake muons.
In this post I would like to discuss the last category among the four listed above: nuclear interactions in the detector material. In a future post of this series we will see why this potential
source of background, together with muonic decays in flight of long-lived hadrons (essentially kaons and pions, ,
and their charge-conjugate reactions), is particularly important to understand.
Now, the CDF tracker is built with light materials: a thoughtful effort during design and construction was made to insert as little matter as possible, in order to minimize several effects known to worsen the detector performance in terms of momentum resolution, tracking efficiency, occupancy, and other parameters. The most important of these effects are multiple scattering, photon conversions, and indeed, nuclear interactions.
[Incidentally, little material is a good thing, but zero material would be a disaster! In vacuum, charged particles cannot be tracked, because there are no atoms to ionize, and without ionization, the particle path cannot be reconstructed. Gaseous mixtures work well for that purpose, allowing a measurement which does not affect the particle momenta appreciably. But other, more aggressive designs, are possible: silicon wafers throughout the tracker volume, as in the CMS detector, or scintillating fibers, as in the D0 tracker, are two meaningful alternatives.]
So, let me discuss below shortly the three processes mentioned above, for a start.
Multiple scattering affects all electrically charged particles. It is the combined result of all electromagnetic interactions between a charged particle and the atoms of the traversed medium: a cumulative effect that produces a deviation from the original direction of the particle. The deviation increases with the square root of the depth of material traversed, pretty much as random walk, brownian motion, and similar diffusion processes. Multiple scattering is mostly relevant for low-momentum particles, whose trajectory can be affected by relatively small forces.
Photon conversions are instead the result of the process called “pair production”, which is of course only relevant to, well, photons. Since, however, photons are the inevitable result of neutral pion decay (), they are actually quite frequent in hadronic collisions, and their phenomenology cannot be ignored. A relativistic photon in vacuum cannot materialize into an electron-positron pair, because it cannot simultaneously conserve energy and momentum in the process; however, the pair creation may occur in the presence of a static source of electromagnetic field, like a heavy nucleus, which absorbs the needed recoil. The thicker with heavy nuclei a particle tracker is, the harder it is for energetic photons to dodge nuclei, wading their way through the tracker and into the surrounding electromagnetic calorimeter, where they are finally encouraged to convert by lead nuclei. In the
calorimeter, pair production and electron bremsstrahlung cause the creation of a cascade, enabling a measurement of the photon’s energy. In principle, the detection of energetic photons, which are quite interesting particles at a collider for a number of reasons, could also happen by the identification of the pair-produced electron and positron in the tracker, but this is less efficient and the produced pairs would increase the detector occupancy, hindering the reconstruction of the events.

[In the figure on the right is shown the distribution of the radius (transverse distance from the beam line) where a photon conversion originated an electron-positron pair inside the CDF tracker. You see spikes at radii where material is concentrated: these are the silicon ladders and support structures, and the inner wall of the COT cylinder (on the right). As you see, photon conversions really provide a radiography of the tracker.]
Finally, nuclear interactions are the means by which the energy of hadrons -both charged and neutral, this time- is measured in hadronic calorimeters. They occur when a hadron hits directly a nucleus of the “absorber” -the passive material used in those devices-, thereby producing a few additional hadrons by strong interaction. These secondary particles may in turn hit other nuclei, with the generation of a hadronic cascade. Like photon conversions, nuclear interactions are to be avoided inside the tracker, because they confuse the event reconstruction. And like conversions, nuclear interactions depend on the amount of nuclear matter. A slight difference exists: conversions, being sensitive to the electrical field of the nucleus, increase with the atomic number Z; nuclear interactions instead depend on the number of nucleons, A. But this is a detail…
Now, if we suppose for a moment that energetic hadrons hitting the detector material contained inside the tracker volume (ladder support structures of the silicon microvertex detector, or the silicon wafers themselves, wires in the tracking chamber, or the inner cylinder of the vessel) are capable of creating showers of secondaries -well, let’s say at least pairs of them-, and if we further imagine that some of those secondaries will produce punch-through (hadrons managing to traverse the calorimeter and leave a signal in the muon chambers), we get a mundane physical process which creates muon candidates with large impact parameter: a large impact parameter is guaranteed by the fact that the secondary interactions occur several centimeters away from the primary interaction point, and any secondary particle emitted at even small angle from the direction of the incoming hadron would not point back to the primary interaction point.
It is to be noted that if hadronic nuclear interactions produced a sizable amount of punch-through in our data we would automatically have an excess of “ghost” muons, because the sample composition, extracted from events where the muons left hits in the inner silicon layers, would not include these “secondary muons”, and an extrapolation towards muons with no inner SVX hits would fail to account for the total, leaving a deficit equal to the size of that background.
It must also be stressed that, in principle, we know that the above hypothesis -nuclear secondaries making it to the muon detector in numbers- is on shaky ground from the outset. That is because nuclear interactions are kept at a minimum by the way the tracker
is built. We know the amount of material we have used to build the tracker: we have weighted on a scale the darn thing before inserting it inside the solenoid! Moreover, we have conversions, as shown in the plot above, and they cannot lie.
The authors of the multi-muon analysis have studied this background with care anyway. They took all the muons in the sample, and paired each of them up with any track contained in a 40 degree cone around them. Then, the pair was required to have a common origin: with two three-dimensional paths, the best way to check this is to “fit” the two paths together, finding the most likely point in space from where they may have originated. Of course, most pairs of tracks miss each other by kilometers, but a few do fulfil the requirement. This may be due to sheer chance -after all, each muon may be paired with several tracks-, to the two-body decay of a parent particle (we saw two examples in part 2 of this series: and
, where the muon takes the role of one pion), and to nuclear interactions. In the latter case, the muon is a punch-through hadron, by construction: nuclear interactions do not yield real muons!
Once a sample of well-fitting pairs was collected, the authors studied the distance R from the beam line of the point of origin of the pair. While neutral kaons and lambda decays should show an exponential tail in R, nuclear interactions should show spikes in correspondence to the concentrations of nuclear matter, in close similarity to the conversion radius plot shown at the beginning of this post.
The R distributions for muons with hits in the inner silicon layers is shown in the first graph below, while the R distribution for events belonging to the “ghost” sample is shown in the second one.


Let me now try to explain the shape of these distributions.
First of all: what do negative R values mean ??? R is defined as negative when the vertex between the muon and the paired particle occurs on the emisphere opposite to the one containing the muon. The emisphere is centered on the primary interaction vertex: a negative R means that the two tracks have been paired by chance, because there is no known physics that allows a particle to be created in a proton-antiproton collision at the center of the detector, travel one way, decay or interact with a nucleus, and produce two other particles in the opposite direction: momentum must be conserved in the interaction that produced the two vertexed particles!
Second: you observe that R values consistent with zero are the most likely. This is not surprising: most of the tracks in any proton-antiproton collision come from the primary vertex (R=0), so casual combinations of these tracks with muon tracks will favor that radius for the two-track vertex, unless muons are heavily displaced from it. [While the ghost sample does exhibit a very long tail in the impact parameter distribution, there are many of them with a small value of that quantity: the ghost sample is indeed estimated to be contaminated with non “exotic” background sources, and these will have a peak at zero impact parameter regardless of the silicon hits they possess.]
Third: you get a rapidly falling distribution in R, for both positive and negative R. This also is due to the fact observed above, that random tracks primarily come from the primary interaction vertex. Actually, since combinatorics should create two equally populated tails on positive and negative values of R, you get to size up the “excess” of vertices at positive R, which is due
to the combination of nuclear interactions AND V-particle decays ( and
), the background we have discussed in part II of this series. For ghost events, V-particle decays contribute about 8%. It is quite unfortunate that a plot of the R distribution for background-subtracted V-particle vertices has not been produced, and overimposed -or subtracted- to the distributions shown above. However, I have to give it to the authors: it is an irrelevant issue. What these plots tell us is that…
Fourth: there are no spikes in these distributions. They are smoothly falling, indicating that there are no concentrations of locations, at fixed R, around the beam pipe from which multiple
hadrons originate. The observation is meaningful, because we know that the material in the tracker is concentrated at very particular values of R -a result of having designed the detector with a roughly cylindrical symmetry around the beam axis. The distributions shown above do not exclude that nuclear interactions may contribute with punch-through muons, because elastic interactions, which are by no means rare, would not appear as two-track vertices; the same can be said of ones producing only one charged hadron plus several neutral ones.
Because of that, nuclear interactions affect the estimate of the ghost component of dimuon data in a way not easy to size up. If the ghost sample was only a numerical excess of muons with very large impact parameter, the case would be closed here: Occam’s razor would force us to stick to known sources to explain our observations, and no new physics could be invoked by a reasonable physicist. However, in the following parts of this multi-thread post we will come to finally discuss the characteristics that make multi-muon events anomalous stuff: the fact that they, indeed, contain multiple muons; and that these additional muons won’t listen to QCD predictions as far as their impact parameter, or the invariant mass they make with the
triggering muon, are concerned.
Some notes on the multi-muon analysis – part II November 8, 2008
Posted by dorigo in news, physics, science.Tags: anomalous muons, CDF, new physics
comments closed
In this post, as I did in the former one, I discuss a self-contained topic relevant for the estimation of mundane sources of “ghost” muons, the anomalous signal recently reported by CDF in data collected in proton-antiproton collisions at 1.96 TeV, generated by the Tevatron collider in Run II. The data have been acquired by a dimuon trigger, a set of hardware modules and software algorithms capable of selecting in real time the collisions yielding two muons of low transverse momentum.
The transverse momentum of a particle is the component of its momentum in the direction orthogonal to the proton-antiproton beams. In hadronic collisions, large transverse momentum is a telling feature: the larger are transverse momenta of particles, the more violent was the interaction that generated them. In contrast, the longitudinal component of momentum is incapable of discriminating energetic collisions from soft ones, because the collisions involve quarks and gluons rather than protons and antiprotons. Quarks and gluons carry a unknown fraction of their parent’s momentum, and they generate collisions whose rest frame has a unknown, and potentially large longitudinal motion. Imagine a 100 mph truck hitting a 10mph bicycle head-on: after the collision the bicycle, and maybe a few glass pieces from a front lamp of the truck, will be found moving in the original direction of the truck, with a speed not too different from that of the truck itself. In contrast, when two 100 mph trucks hit head-on, you will be likely to find debris flying out at high speed in all directions. The transverse speed of the debris is a tale-telling sign that an energetic collision happened, while the longitudinal one is much less informative.
The reason why above I made sure you understood the importance of transverse momentum is that I am going to use that concept below, to explain what may mimic a muon signal in the CDF detector -an issue of crucial relevance to the multi-muon analysis. If you do not know what the multi-muon analysis is about, I suggest you go back to read the former post, and maybe the first one announcing the new CDF preprint. Otherwise, please stay with me.
Now, the dimuon trigger works by selecting events with two charged tracks pointing at hits in the CMU and CMP muon chambers, which are detectors located on the outside of the CDF central calorimeter -a large cylinder surrounding the interaction point, the tracker, and the solenoid which produces the axial magnetic field in which charged particles are made to bend in proportion to their transverse momentum. The dimuon trigger also applies loose requirements on the transverse momentum of the two tracks: 3 GeV or more. By comparison, the single muon trigger used by CDF to collect W and Z boson decays requires transverse momenta in excess of 18 GeV. The loose threshold of the dimuon trigger is possible because of the rarity of two independent, coincident signals in the muon chambers: a single muon trigger with a 3 GeV threshold would instead totally drown the data aquisition system.
Muons are minimum-ionizing particles, and given their momentum we know pretty well how deep they can reach inside the lead and iron which compose the calorimeters: as drivers short of gas, they gradually lose their momentum at a well-defined rate by ionizing the surrounding medium, and they eventually stop. The CMU detectors -wire chambers which indeed detect “hits”, i.e. localized ionization left by muon tracks- are surrounded by 24 inches of steel, and on top of that thick shield lies a second set of muon detectors, the CMP chambers. Muons need at least 2 GeV of transverse momentum to reach the CMU and leave hits there, or at least 3 GeV to make it to the CMP system and leave a signal there as well. When they do, they get to be called “CMUP muon candidates”. A muon candidate which leaves a signal in both the CMU and CMP chambers is a very, very clean one: as good as it gets in CDF.
Why do I insist in calling muons “candidates”, in the face of the cleanness of CMUP muons ? Because a muon signal at a hadron collider will always be plagued with background from hadrons punching through the calorimeter, producing muon chamber hits and thus faking real muons. Hadrons, unlike muons, are made of quarks, and so they cannot traverse large amounts of dense matter unscathed. As they leave the interaction point and enter the calorimeters, most of the times hadrons hit a heavy nucleus, producing some downstream debris which in turn gets absorbed by other nuclei. Thus, because hadrons are not minimum-ionizing particles, they have a much harder time than muons to reach the CMU detector, and a harder time still to make it to the CMP. Despite that, hadrons are so copiously produced in proton-antiproton collisions that one of them occasionally punches through the calorimeter system and reaches the CMU or the CMP detectors: the rarity of the punching through the calorimeter is compensated by the enormous rate with which hadrons enter it.
Now, if muons may be faked by hadrons, one has to reckon with the possibility that the “ghost” sample evidenced by CDF -muon candidates with abnormally large impact parameters, I venture to remind- may be composed, or at least contaminated, by hadrons with very large impact parameter. Hadrons with very large impact parameter ? This immediately brings a particle physicist to think of short K-zeroes and Lambdas!
Short K-zeroes, labelled , have a lifetime of about a tenth of a nanosecond. They may thus travel several centimeters in the CDF tracker before disintegrating into a pair of charged pions,
(a relativistic particle makes a bit less than 30 centimeters in a nanosecond). These pions will have definitely a large impact parameter. Now, imagine it is a lucky day for one of these pions: it gets shot through the calorimeter by the kaon decay, and it sees heavy nuclei whizzing around as it plunges deep in the dense matter. After dodging billions of nuclei, and losing energy at a rate not too different from that of a muon through ionization of the medium, it makes it to the CMU chamber, leaves a hit there, enters the 24 inches of iron shield, dodges a few billion more nuclei, and makes it through the CMP too, creating further hits! A CMUP muon candidate!
The same mechanism discussed above can in principle provide a large impact parameter muon candidate through the decay to a proton-pion pair, : here the negative pion may be the hero of the day. Lambdas have a lifetime of 0.26 nanoseconds: together with short K-zeroes, these particles were called “V-particles” in the fifties, because they appeared as V’s in the bubble chamber pictures, such as the one below.

[In this picture we see the process called “associated production of strangeness”. The strong interaction of a negative pion (the track entering from the left which disappears) with a proton at rest produces two strange particles -a anti-kaon and a Lambda, which produce the two “V’s”. The reaction is . I remind you that the anti-kaon has the quark content
, while the Lambda is a
triplet. Strong interactions conserve additively the strangeness quantum number, and since S=0 in the initial state, S must be zero after the strong collision, so the S=+1 of the Lambda must be balanced by the S=-1 of the anti-kaon. Also, note that the weak decay of the two strange particles violates strangeness conservation: at the end of the chain, we are left with no strange particles!]
 How to estimate the background due to V particles to the ghost muon signal ? Again, we use the very same dimuon data containing ghost events. We take a muon candidate and pair it up with any oppositely-charged track detected in the CDF tracker. We only care to select pairs which may have a common point of origin, and this fortunately reduces quite a bit the combinatorics. What do we make of these odd pairs ? We assume that the muon is in truth a charged pion, and that the other particle too is a pion, and we proceed to verify whether they are the product of the decay of a
How to estimate the background due to V particles to the ghost muon signal ? Again, we use the very same dimuon data containing ghost events. We take a muon candidate and pair it up with any oppositely-charged track detected in the CDF tracker. We only care to select pairs which may have a common point of origin, and this fortunately reduces quite a bit the combinatorics. What do we make of these odd pairs ? We assume that the muon is in truth a charged pion, and that the other particle too is a pion, and we proceed to verify whether they are the product of the decay of a . Lo and behold, we do see a peak in the pair’s invariant mass distribution, as shown in the plot on the right! The peak sits at the 495 MeV mass of the neutral kaon, as it should, and has the expected resolution.
“Now wait a minute,” I can hear the courageous reader who reached this deep into this post say, “you said you took a muon and a pion and made a mass with them, and you find a K-zero ? But K-zeroes do not make muons!”. Sure, of course. That is the whole point: the muon candidates which belong to the nice gaussian bump shown in the plot are not real muons, but heroic pions that made it through the calorimeter: fake muons!
 A similar procedure produces the plot shown on the left, where this time we tentatively assigned the proton mass to the other track. A sizable
A similar procedure produces the plot shown on the left, where this time we tentatively assigned the proton mass to the other track. A sizable signal appears on top of a largish combinatorial background!
We are basically done: we count how many V particles we found in the data, we divide this number by the efficiency with which we find the V’s once we have one leg in the muon system (a number which the Monte Carlo simulation cannot get wrong too much, and which is roughly equal to 50%), and we get an estimate of the number of ghost muons due to hadron punch-through with lifetime. Since there are about 5300 kaons and 700 lambdas, this makes an estimate of about 6000/0.5 = 12,000 fake muons in the ghost sample: about 8% of the original signal.
Actually, we can be even tidier than just counting fake muons. We can play a nice trick that experimental particle physicists find elegant and simple. You see the mass distribution for the kaon signal above ? Imagine you make three vertical slices around the kaon: a central one including the gaussian bump, and two lateral ones half as wide. To be precise, let us say we select events with as the left sideband; events with
as the signal band, and <
as the right sideband. To first approximation, the number of non-kaon track pairs making the two “sidebands” is equal to the number of non-kaon track pairs in the central band, because they approximately contain the same number of events, once you neglect the gaussian signal -which is due to kaons. The approximation amounts to assuming that the background has a constant slope: certainly not far from the truth.
 Now, you can take the events in the central band, and create a distribution of the impact parameter of the muon candidate track they contain (a sure fake muon, for the K signal; and a regular muon for the rest of the events). Then, you can take the sidebands and make a similar distribution with the muon candidates those sideband events contain. Finally, you can subtract this second impact parameter distribution (non-classified muons) from the first one (certified fake muons). Mind you, it will not happen frequently to you to subtract signal from a background to study the background -it usually happens the other way around! In any case, what you are left with is an histogram of the impact parameter distribution expected from fake muons from hadronic punch-through with large impact parameter. Neat, ain’t it ?
Now, you can take the events in the central band, and create a distribution of the impact parameter of the muon candidate track they contain (a sure fake muon, for the K signal; and a regular muon for the rest of the events). Then, you can take the sidebands and make a similar distribution with the muon candidates those sideband events contain. Finally, you can subtract this second impact parameter distribution (non-classified muons) from the first one (certified fake muons). Mind you, it will not happen frequently to you to subtract signal from a background to study the background -it usually happens the other way around! In any case, what you are left with is an histogram of the impact parameter distribution expected from fake muons from hadronic punch-through with large impact parameter. Neat, ain’t it ?
The impact parameter distribution is shown in the plot on the right above. Observe that these V-particle decays (hyperons have been also added to the distribution shown) do produce muon candidates with quite large impact parameters: I remind you that B-hadrons have died out when the impact parameter is larger than about five millimeters. Is this the source of ghost events ? Well, yes, 8% of it. In the CDF article, the authors are careful to explain from the outset that they treat ghost muons as a unidentified background, and they proceed to try and explain it away -eventually failing. Well: the simple punch-through mechanism discussed here accounts for 8% of it, but not much more.
 The plot of the impact parameter of fake muons from hadron punch-through seen above can be directly compared with the plot of impact parameters of ghost muons, since both the x-axis and the y-axis have the same boundaries. I attach the original ghost-muon IP plot on the left, so that one can compare the two effortlessly. You can see that while the distribution of impact parameter is not too different in the two plots, the ghost muons (black points here) are more than one order of magnitude more numerous, especially at large impact parameters.
The plot of the impact parameter of fake muons from hadron punch-through seen above can be directly compared with the plot of impact parameters of ghost muons, since both the x-axis and the y-axis have the same boundaries. I attach the original ghost-muon IP plot on the left, so that one can compare the two effortlessly. You can see that while the distribution of impact parameter is not too different in the two plots, the ghost muons (black points here) are more than one order of magnitude more numerous, especially at large impact parameters.